Depth First Search Algorithm

The DFS algorithm is a recursive algorithm that uses the idea of backtracking. It involves exhaustive searches of all the nodes by going ahead, if possible, else by backtracking. Here, the word backtrack means that when you are moving forward and there are no more nodes along the current path, you move backwards on the same path to find nodes to traverse. All the nodes will be visited on the current path till all the unvisited nodes have been traversed after which the next path will be selected. This recursive nature of DFS can be implemented using stacks.

As the name DFS suggests, you are required to traverse the graph depthwise as follows:

1. Pick a starting node and push all its adjacent nodes (if not seen previously) into a stack.
2. Pop a node from stack to select the next node to visit and push all its adjacent nodes into a stack.
3. Repeat this process until the stack is empty.

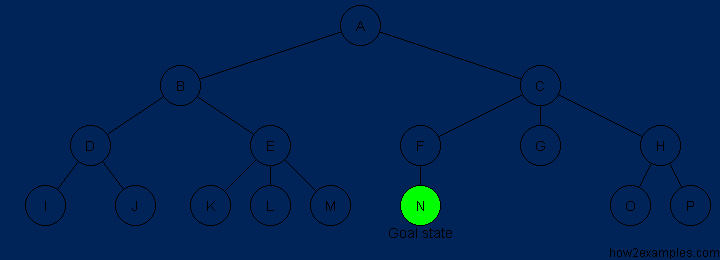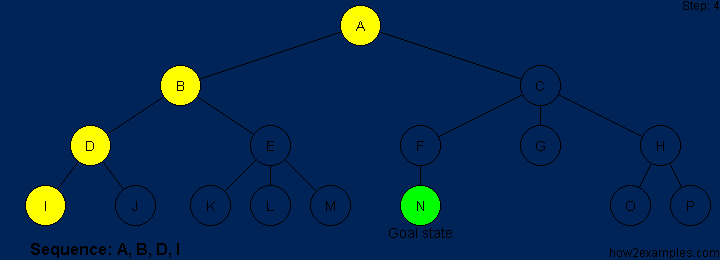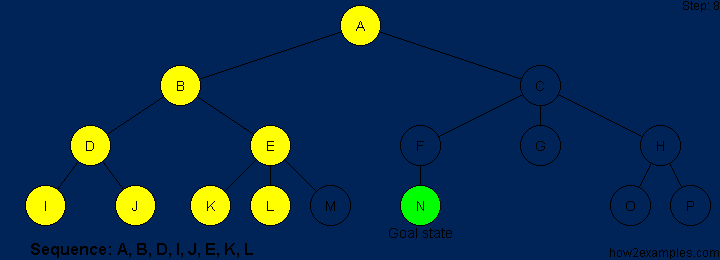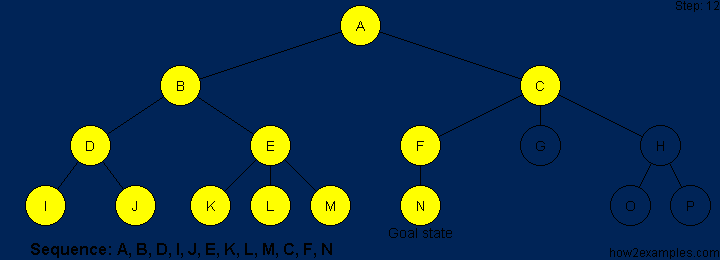
The steps are shown above graphically in sequence

Unlike breadth-first search, depth-first search is not guaranteed to find the solution with the shortest path. As it is possible for depth-first search to proceed down an infinitely long branch, without ever returning to explore other branches, there is no guarantee that depth-first search will ever find a solution, even when one exists. The memory requirements of depth-first search are more modest than breadth-first search. Only a single path from the root node to the current node, plus any unexpanded nodes on the path, need to be stored.

Psuedocode

                    Input: s as the source node

                    DFS(G, u)
                        u.visited = true
                        for each v ∈ G.Adj[u]
                            if v.visited == false
                                DFS(G,v)
     
                    init() 
                        For each u ∈ G
                            u.visited = false
                        For each u ∈ G
                            DFS(G, u)