Breadth First Search Algorithm

BFS is a traversing algorithm where you should start traversing from a selected node (source or starting node) and traverse the graph layerwise thus exploring the neighbour nodes (nodes which are directly connected to source node). You must then move towards the next-level neighbour nodes.

As the name BFS suggests, you are required to traverse the graph breadthwise as follows:

1. First move horizontally and visit all the nodes of the current layer
2. Move to the next layer

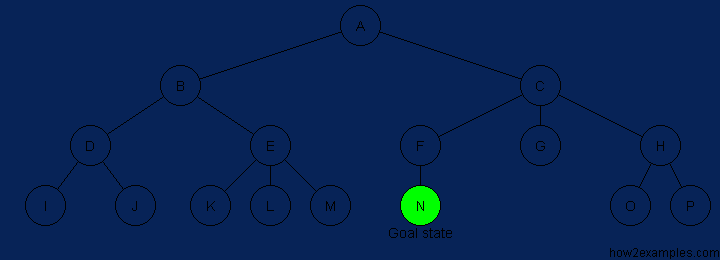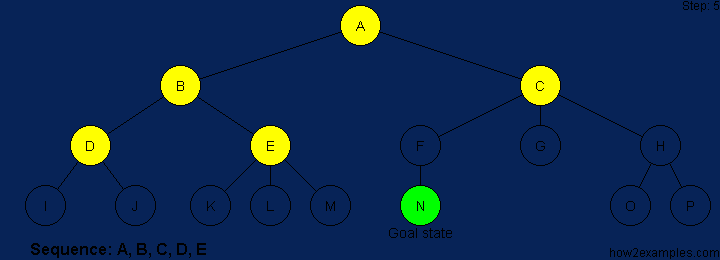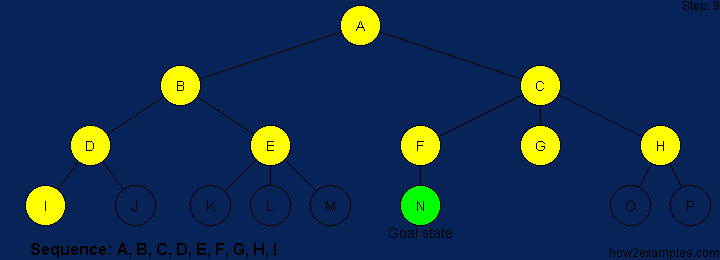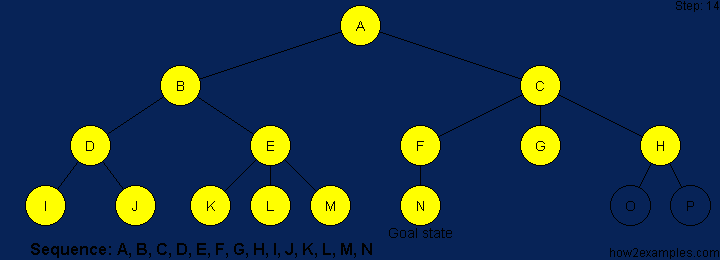
The steps are shown above graphically in sequence

As breadth-first search exhaustively examines every node at a particular depth before progressing to the next level, it is guaranteed to find the solution, if one exists, with the shortest path from the initial state. A disadvantage of breadth-first search is that it can have a high memory requirement - as a record needs to be maintained of every expanded node.

Psuedocode

                    Input: s as the source node
 
                    BFS (G, s)
                        let Q be queue.
                        Q.enqueue(s)
                         
                        mark s as visited
                        while (Q is not empty)
                            v = Q.dequeue()
                         
                        for all neighbors w of v in Graph G
                            if w is not visited
                                Q.enqueue(w)
                            mark w as visited